კრიტერიუმის სტატისტიკის ის მნიშვნელობები, რომლებიც იძლევა ნულოვანი ჰიპოთეზის უარყოფის საფუძველს. ყველა ასეთ მნიშვნელობათა სიმრავლეს უარყოფის არე ეწოდება. უარყოფის არის ასაგებად, უნდა დავადგინოთ კრიტერიუმის სტატისტიკის რომელი მნიშვნელობები არ არის მოსალოდნელი იმ შემთხვევაში, როცა ნულოვანი ჰიპოთეზა სამართლიანია.
უარყოფის არე დამოკიდებულია:
- კრიტერიუმის სტატისტიკის განაწილებაზე;
- განაწილების რომელი კუდები იქნება გამოყენებული ანუ ორმხრივია თუ ცალმხრივი ალტერნატივა;
- ამ კუდებში მოხვედრის ალბათობებზე.
მაგალითი: გვაქვს n=49 დაკვირვება, რომელთა საშუალო და სტანდარტული გადახრაა შესაბამისად და S=1.1.
ნულოვანი ჰიპოთეზაა
თუ ნულოვანი ჰიპოთეზა ჭეშმარიტია, შერჩევის საშუალო საკმაოდ ახლოს უნდა იყოს 3.8-თან. თუ მანძილი შერჩევით და ჰიპოთეტურ საშუალოებს შორის დიდია, მაშინ კრიტერიუმის სტატისტიკის გამოთვლილი მნიშვნელობა ახლოს იქნება ამ სტატისტიკის განაწილების რომელიმე კუდთან (მარჯვენა ან მარცხენა კუდთან). კრიტერიუმის სტატისტიკა ამ ჰიპოთეზისათვის არის:
რადგან n=49>30, ამიტომ Z-ს აქვს სტანდარტული ნორმალური განაწილება N (0,1).
ალტერნატიული ჰიპოთეზისათვის არსებობს სამი შესაძლებლობა:
ვთქვათ, ალტერნატივაა თუ ის სამართლიანია, მაშინ მოსალოდნელია, რომ სხვაობა დიდია, შესაბამისად, დიდი იქნება Z და ნულოვანი ჰიპოთეზის უარყოფის არე აღმოჩნდება Z-ის განაწილების მარჯვენა კუდში ანუ ექნება სახე . ასეთ კრიტიკულ არეს ეწოდება მარჯვენა ცალმხრივი.
რიცხვს ვირჩევთ ისე, რომ თუ სამართლიანია, მაშინ Z სტატისტიკის -ში მოხვედრის ალბათობა იყოს რაც შეიძლება მცირე, მაგალითად 0.01, 0.05 ან 0.1. ამ ალბათობას მნიშვნელოვნების დონე ეწოდება და ის აღინიშნება ასოთი.
რიცხვს ვპოულობთ სტანდარტული ნორმალური განაწილების ცხრილიდან, მაგალითად, თუ ამ შემთხვევაში და რადგან Z=3.18>1.65, ამიტომ ჰიპოთეზას უარვყოფთ და -ს ვღებულობთ.
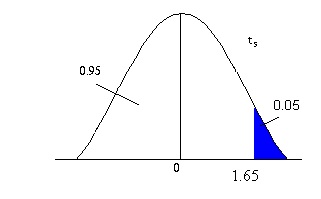
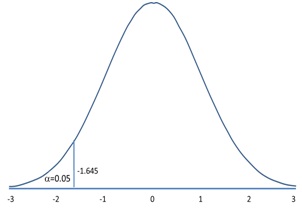
თუ ალტერნატივაა ნულოვანი ჰიპოთეზის უარყოფის არეს ავიღებთ განაწილების მარცხენა კუდში ანუ ინტერვალს ასეთ კრიტიკულ არეს ეწოდება მარცხენა ცალმხრივი. მაგალითად, თუ ამ შემთხვევაში
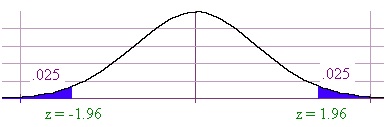
თუ (ორმხრივი კრიტიკული არე) მაშინ უარყოფის არეს ავიღებთ განაწილების ორივე კუდში ანუ ორ ინტერვალს და . მაგალითად, თუ ამ შემთხვევაში და . შევნიშნოთ, რომ ორმხრივი კრიტიკული არის დროს თითოეულ ინტერვალში კრიტერიუმის სტატისტიკის მოხვედრის ალბათობაა , ამ შემთხვევაში 0.025.
***
გამოყენებული ლიტერატურა:
Field, A. (2013). Discovering Statistics Using IBM SPSS Statistics. SAGE Publications Ltd.
კისი, ჰ. (2008). სტატისტიკა სოციალურ მეცნიერებებში. სოციალურ მეცნიერებათა ცენტრი. თბილისის უნივერსიტეტის გამომცემლობა
