ზარისებური ფორმის სიხშირეთა ალბათური განაწილება მიიღება მაშინ, თუ მონაცემთა უმრავლესობა გროვდება განაწილების ცენტრში და იკლებს ცენტრიდან მოშორებით. ნორმალური განაწილება რეალური სამყაროს ერთ-ერთი ყველაზე ხშირად გამოყენებადი მოდელია. ცოცხალი ორგანიზმების პოპულაციაში ბევრ სხვადასხვა მაჩვენებელს აქვს ზარისებური ფორმის განაწილება. მაგალითად, სტატისტიკოსების მონაცემებით, ინგლისელი მამაკაცების უმრავლესობის სიმაღლე ახლოსაა 175 სმ-თან, ცოტაა ძალიან მაღალი მამაკაცი, რომლის სიმაღლე მეტია 205 სმ-ზე და ძალიან დაბალი, სიმაღლით ნაკლები 145 სმ-ზე. 99.9% ინგლისელი მამაკაცების სიმაღლე მოქცეულია ინტერვალში 145 – 205 სმ.,  სიმაღლეების  68% ინტერვალში 165 – 185 სმ. იმისათვის, რომ ავაგოთ ნორმალური განაწილების გრაფიკი უნდა ვიცოდეთ ამ განაწილების საშუალო (ცენტრი, $\mu$) და განაწილების სტანდარტული გადახრა ($\sigma$). ნორმალურ განაწილებას  ნულის ტოლი საშუალოთი ($\mu =0$) და ერთის ტოლი სტანდარტული გადახრით ($\sigma =1$) ეწოდება სტანდარტული ნორმალური განაწილება. სტანდარტული ნორმალური განაწილება აქვს ე.წ. Z- ქულებს. Z- ქულების 68% „ვარდება“ ინტერვალში  -1-დან + 1-მდე, 95% ინტერვალში (-1.96, 1.96), 99% ინტერვალში (-2.58, 2.58). Z- ქულების მხოლოდ 1% არის  -2.58-ზე ნაკლები ან  2.58-ზე მეტი.

თუ X ცვლადს აქვს ნორმალური განაწილება $\mu$ საშუალოთი და ${\sigma }^2$ დისპერსიით, ეს ფაქტი აღინიშნება როგორც $X~N(\mu ,{\sigma }^2)$. $\mu$ და ${\sigma }^2$- ნორმალური განაწილების პარამეტრებია. ნორმალური განაწილება სრულად აღიწერება, თუ ცნობილია $\mu$ და $\sigma$. ნორმალური განაწილების სიმკვრივის გრაფიკები პარამეტრის სხვადასხვა მნიშვნელობისათვის მოცემულია ქვემოთ. 

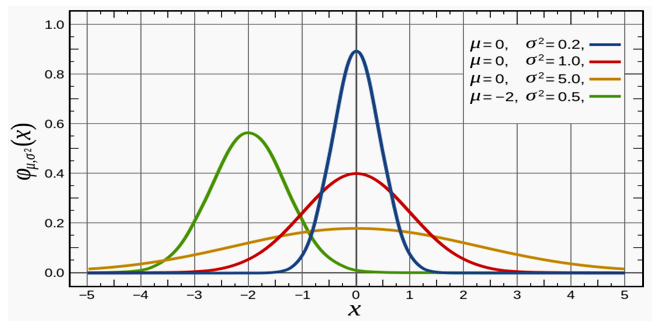
ალბათობების გამოსათვლელად არ არის აუცილებელი ბევრი ცხრილის  შექმნა ($\mu ,\sigma$) სხვადასხვა წყვილისათვის, რადგან ნებისმიერი ნორმალური განაწილება შეიძლება, გადაყვანილი იქნეს სტანდარტულ ნორმალურ განაწილებაში N (0,1). ამისათვის საჭიროა, მოვახდინოთ X-ის სტანდარტიზაცია ფორმულით: 

$Z=\frac{X-\mu }{\sigma }$  თუ  $X~N(\mu ,{\sigma }^2)$  მაშინ $Z=\frac{X-\mu }{\sigma }~N(0,1)$. 

Z აქვს სტანდარტული ნორმალური განაწილება ნულის ტოლი საშუალოთი და ერთის ტოლი დისპერსიით. 

***

გამოყენებული ლიტერატურა:

Field, A. (2013). Discovering Statistics Using IBM SPSS Statistics. SAGE Publications Ltd.

კისი, ჰ. (2008). სტატისტიკა სოციალურ მეცნიერებებში. სოციალურ მეცნიერებათა ცენტრი.  თბილისის უნივერსიტეტის გამომცემლობა