შეფასება ჩაუნაცვლებელია, თუ მისი მნიშვნელობების საშუალო არითმეტიკული, გამოთვლილი უსასრულოდ ბევრი შერჩევიდან შესაფასებელი პარამეტრის მნიშვნელობის ტოლია. სხვა სიტყვებით  ჩაუნაცვლებლობა გულისხმობს შემდეგს, მიუხედავად იმისა, რომ სხვადასხვა შერჩევის მიხედვით, გამოთვლილი პარამეტრის შეფასება საზოგადოდ განსხვავებულ შედეგებს იძლევა, ის საშუალოდ მაინც ემთხვევა პარამეტრის ჭეშმარიტ მნიშვნელობას.  შერჩევითი საშუალო წარმოადგენს პოპულაციის საშუალოს საუკეთესო შეფასებას, იმ გაგებით რომ ის არის ჩაუნაცვლებელი შეფასება, შერჩევის დისპერსია კი არ წარმოადგენს პოპულაციის დისპერსიის ჩაუნაცვლებელ შეფასებას, ის ჩანაცვლებული შეფასებაა.

მოვიყვანოთ საილუსტრაციო მაგალითი იმისა, რომ შერჩევითი საშუალო ჩაუნაცვლებელი შეფასებაა, ხოლო შერჩევითი დისპერსია კი ჩანაცვლებული.

დავუშვათ, რომ პოპულაცია შეიცავს სამ მონაცემს {0, 2, 4} და მისგან ვაკეთებთ  n=2 მოცულობის შერჩევებს. პოპულაციის საშუალო $\mu =\frac{0+2+4}{3}=2$ ხოლო პოპულაციის დისპერსია ${\sigma }^2=\frac{1}{3}\left[(0-2{)}^2+(2-2{)}^2+(4-2{)}^2\right]=\frac{8}{3}$. ყველა შესაძლო შერჩევათა რაოდენობა იქნება (შერჩევის როგორც პირველი, ისე მეორე ელემენტი შესაძლო მნიშვნელობათა რაოდენობა 3-ის ტოლია) ამოვწეროთ ეს შერჩევები და გამოვთვალოთ მათი საშუალოები და დისპერსიები. შედეგები მოცემულია ცხრილში: 

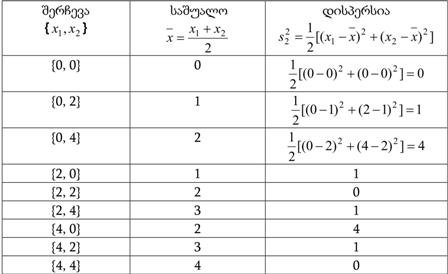
 აქედან გამომდინარე, შერჩევითი საშუალოების საშუალო $\frac{0+1+2+!+2+3+2+3+4}{9}=2$ იქნება, ხოლო დისპერსიების საშუალო კი $\frac{0+1+4+1+0+1+4+1+0}{9}=\frac{4}{3}$. როგორც ვხედავთ, შერჩევითი საშუალო პოპულაციის საშუალოს ჩაუნაცვლებელი შეფასებაა, შეჩევითი დისპერსია კი პოპულაციის დისპერსიის არა. სინამდვილეში $\frac{4}{3}=\frac{2-1}{2}·\frac{8}{3}=\frac{n-1}{n}·\frac{8}{3}$ და შესწორება ხდება სწორედ $\frac{n-1}{n}$ -ის შებრუნებული სიდიდით $\frac{n}{n-1}$  რათა მივიღოთ ჩაუნაცვლებელი შეფასება $\frac{8}{3}=\frac{n}{n-1}\frac{4}{3}$.

***

გამოყენებული ლიტერატურა:

Field, A. (2013). Discovering Statistics Using IBM SPSS Statistics. SAGE Publications Ltd.

კისი, ჰ. (2008). სტატისტიკა სოციალურ მეცნიერებებში. სოციალურ მეცნიერებათა ცენტრი.  თბილისის უნივერსიტეტის გამომცემლობა