ახასიათებს განაწილების კონცენტრაციის ხარისხს მოდის მიდამოში ანუ გვიჩვენებს, რამდენად წამახვილებულია განაწილების პიკი. შერჩევითი ექსცესის კოეფიციენტი გამოითვლება ფორმულით:

$$e = \frac{{\frac{1}{n}\sum\limits_{i = 1}^n {{{({x_i} - \bar x)}^4}} }}{{{{\left( {\sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {{{({x_i} - \bar x)}^2}} } } \right)}^4}}} - 3.$$

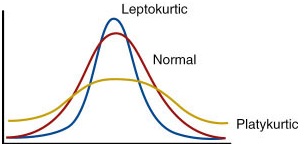
ექსცესის კოეფიციენტისთვის ყოველთვის სამართლიანია $e\mathit{\ge }\mathit{-}\mathit{2}$. ნორმალური განაწილებისათვის ეს კოეფიციენტი ნულის ტოლია. რაც უფრო დიდია e, მით მეტადაა კონცენტრირებული (წამახვილებული) განაწილება მოდის მიდამოში ანუ განაწილების გრაფიკს აქვს მაღალი პიკი და, პირიქით, თუ e პატარაა - პიკი დაბალია. როცა e>0 განაწილებას მოდის მიდამოში უფრო მაღალი და მახვილი პიკი აქვს, ვიდრე ნორმალურ განაწილებას, ხოლო თუ e<0 პიკი უფრო დაბალი და გლუვია, ვიდრე ნორმალური განაწილების.  

***

გამოყენებული ლიტერატურა:

Field, A. (2013). Discovering Statistics Using IBM SPSS Statistics. SAGE Publications Ltd.

კისი, ჰ. (2008). სტატისტიკა სოციალურ მეცნიერებებში. სოციალურ მეცნიერებათა ცენტრი.  თბილისის უნივერსიტეტის გამომცემლობა