თუ მონაცემები დალაგებულია ზრდის მიხედვით, მედიანა ყოფს მათ ორ ტოლ ნაწილად. მედიანა საშუალოსთან შედარებით უფრო კარგი ტიპური მნიშვნელობაა იმ შემთხვევაში, როცა სიხშირეთა განაწილება ძალიან ასიმეტრიულია ან მონაცემებს შორის არის ექსტრემალური მნიშვნელობები (ამოვარდნები).
მედიანას თვისებები:
- ისევე როგორც საშუალო, მედიანა გამოიყენება მონაცემებისთვის ინტერვალების და შეფარდების სკალაზე. მედიანა შეიძლება გამოთვლილი იქნეს რიგის სკალის მონაცემებისთვისაც, თუმცა არ შეიძლება მედიანის გამოთვლა სახელდების სკალის მონაცემებისათვის, რადგან არ შეიძლება ამ მონაცემების რანჟირება.
- მედიანის მარჯვენა და მარცხენა მხრიდან მოთავსებულია მონაცემების ტოლი რაოდენობა.
მაგალითი: 7 ადამიანის შემოსავალი არის $10200, 10400, 10700, 11200, 11300, 11500 და 200000. თუ ამ რიცხვებს დავალაგებთ ზრდის მიხედვით, მედიანა, როგორც შუა რიცხვი იქნება 11200 (მონაცემთა რაოდენობა კენტია). ამ შემთხვევაში მედიანა უფრო კარგად აღწერს „ტიპურ“ შემოსავალს, ვიდრე საშუალო, რომელიც არის 37900.
თუ მონაცემთა რაოდენობა ლუწია, მაგალითად 70 77 77 81 84 88 მედიანა არის შუა ორი მონაცემის საშუალო (77 +81)/2=79.
- მედიანა ითვალისწინებს მხოლოდ შუაში მოხვედრილ მონაცემს. ის თითქმის არ იცვლება კიდურა მონაცემების შეცვლის შემთვევაში. მაგალითად, მონაცემების 8 9 10 11 12, მონაცემების 8 9 10 11 100 და 0 9 10 11 200 მედიანა ერთი და იგივეა და 10-ისტოლია.
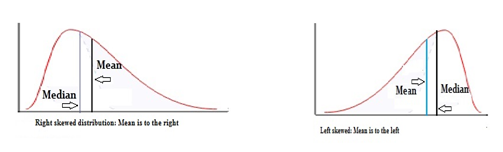
- სიმეტრიული განაწილებისათვის მედიანა და საშუალო ერთმანეთის ტოლია
- მარჯვნივ ასიმეტრიული განაწილებისათვის საშუალო მეტია მედიანაზე, ხოლო მარცხვნივ ასიმეტრიულისათვის კი, პირიქით, საშუალო ნაკლებია მედიანაზე.
მაგალითი: მედიანის გამოთვლა თვისებრივი მონაცემებისათვის.
ცხრილში მოყვანილია შემთხვევით გამოკითხული ადამიანების სიხშირეთა განაწილება მიღებული განათლების მიხედვით.
|
მიღებული განათლება |
სიხშირე |
პროცენტი |
|
დაწყებითი |
38012 |
21,4% |
|
საშუალო |
65291 |
36,8% |
|
კოლეჯი |
33191 |
18,7% |
|
პროფსასწავლებელი |
7570 |
4,3% |
|
ბაკალავრი |
22845 |
12,9% |
|
მაგისტრანტი |
7599 |
4,3% |
|
პროფესორი |
3110 |
1,7% |
|
სულ |
177618 |
|
შერჩევის მოცულობა უდრის n=177618. განმარტებით მონაცემთა ნახევარი ანუ 50% უნდა იყოს მედიანაზე ნაკლები. 21,4% + 36,8% = 58,2% ამიტომ მედიანა ვარდება მეორე კატეგორიაში. ჩვენ შეგვიძლია დავასკვნათ, რომ ამ შერჩევის ნახევარს აქვს მხოლოდ დაწყებითი და საშუალო განათლება.
***
გამოყენებული ლიტერატურა:
Field, A. (2013). Discovering Statistics Using IBM SPSS Statistics. SAGE Publications Ltd.
კისი, ჰ. (2008). სტატისტიკა სოციალურ მეცნიერებებში. სოციალურ მეცნიერებათა ცენტრი. თბილისის უნივერსიტეტის გამომცემლობა
