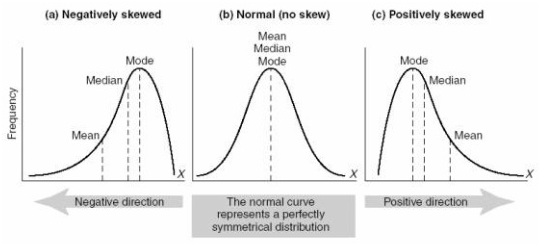
აჩვენებს რამდენად და რა მიმართულებითაა  გადახრილი შემთხვევითი სიდიდის განაწილება სიმეტრიული განაწილებისაგან. შერჩევითი ასიმეტრიის კოეფიციენტი გამოითვლება ფორმულით:

$$a = \frac{{\frac{1}{n}\sum\limits_{i = 1}^n {{{({x_i} - \bar x)}^3}} }}{{{{\left( {\sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {{{({x_i} - \bar x)}^2}} } } \right)}^3}}}$$

თუ შემთხვევითი სიდიდის განაწილება თავისი საშუალოს მიმართ სიმეტრიულია, მაშინ ასიმეტრიის კოეფიციენტი ნულის  ტოლია.  თუ a<0, მაშინ განაწილება მარჯვნივაა  ასიმეტრიული (დადებითი ასიმეტრია), მისი მარჯვენა კუდი უფრო გრძელია,  ვიდრე  მარცხენა, ხოლო a<0 ნიშნავს, რომ განაწილება მარცხნივაა ასიმემეტრიული (უარყოფითი ასიმეტრია) ანუ მარცხენა კუდი უფრო გრძელია, ვიდრე მარჯვენა.  ცხადია, რომ ნორმალური   განაწილებისათვის  a=0.

a<0 a=0 a>0

***

გამოყენებული ლიტერატურა:

Field, A. (2013). Discovering Statistics Using IBM SPSS Statistics. SAGE Publications Ltd.

კისი, ჰ. (2008). სტატისტიკა სოციალურ მეცნიერებებში. სოციალურ მეცნიერებათა ცენტრი.  თბილისის უნივერსიტეტის გამომცემლობა