დაგროვილი სიხშირეების გრაფიკი ინტერვალებში დაჯგუფებული მონაცემებისათვის. შერჩევის მინიმალურ და მაქსიმალურ მონაცემს შორის შუალედი  დავყოთ თანაბარი სიგრძის რამოდენიმე ინტერვალად $x_{min}={\alpha }_0\le x<{\alpha }_1,{\alpha }_1\le x<{\alpha }_2,...{\alpha }_{t-1}\le x\le {\alpha }_t=x_{max}$ ამ ინტერვალებში მოხვედრილი მონაცემების რაოდენობები (სიხშირეები) აღვნიშნოთ შესაბამისად $n_1,n_2,...n_t$ სიმბოლოებით, ცხადია, სადაც შერჩევის მოცულობაა. მოცემული ნამდვილი x რიცხვისათვის განვიხილოთ N(x) ფუნქცია, რომელიც შემდეგნაირად განიმარტება

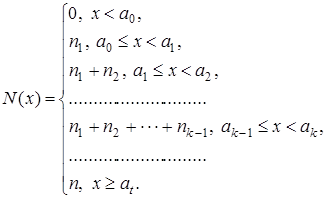
ამ ფუნქციას დაგროვილ სიხშირეთა ფუნქცია ეწოდება. ოგივას ასაგებად Ox ღერძზე აღვნიშნოთ ${\alpha }_0,{\alpha }_1,...{\alpha }_t$ წერტილები და ${\alpha }_1,{\alpha }_2,...{\alpha }_t$ წერტილების თავზე მოვნიშნოთ შესაბამისად $n_1,n_1+n_2,...,n$ სიმაღლეზე წერტილები. შევაერთოთ ეს წერტილები ერთმანეთთან და ასევე $a_0$-თან, მიღებულ ტეხილს ოგივა ეწოდება.  

სურათზე მოცემულია ოგივა გამოცდაზე მიღებული ქულებისათვის. გრაფიკზე წითელი წირის წერტილებში აღნიშნული რიცხვები მიუთითებენ დაგროვილ სიხშირეს ამ წერტილების შესაბამისი აბცისების ტოლი გამოცდის ქულისათვის. მაგალითად, 29 ნიშნავს, რომ 29 ცდის პირის ქულა ტოლია ან ნაკლებია 50-ზე.   

***

გამოყენებული ლიტერატურა:

Field, A. (2013). Discovering Statistics Using IBM SPSS Statistics. SAGE Publications Ltd.

კისი, ჰ. (2008). სტატისტიკა სოციალურ მეცნიერებებში. სოციალურ მეცნიერებათა ცენტრი.  თბილისის უნივერსიტეტის გამომცემლობა