რეალურად პოპულაციის მონაცემები არასოდეს არის ისე ზუსტად სიმეტრიულად განაწილებული, რომ ნორმალურ განაწილებაზე ვისაუბროთ. მაშინ, რატომ არის ნორმალური განაწილება ასეთი მნიშვნელოვანი? ამას ხსნის ცენტრალური ზღვარითი თეორემა (ცზთ): ბევრი დამოუკიდებელი და ერთნაირად განაწილებული შემთხვევითი სიდიდეების ჯამი ან საშუალო არითმეტიკული დაახლოებით ნორმალურადაა განაწილებული.
არ არის ლაპარაკი შემთხვევითი სიდიდეების კონკრეტულ განაწილებებზე, იმისათვის, რომ ცზთ სრულდებოდეს, საჭიროა მხოლოდ ის, რომ შემთხვევითი სიდიდეები დამოუკიდებელი, ერთნაირად განაწილებული და საკმაოდ ბევრი იყოს.
თუ ჩვენ გვაქვს დიდი მოცულობის შერჩევა, მათი საშუალო ნორმალურად იქნება განაწილებული.
მაგალითი: ყუთში 100 ერთნაირი ბურთულაა, გადანომრილი 100-დან 199-მდე. ყუთში ჩაუხედავად ვიღებთ ბურთულას, ვიწერთ მის ნომერს და უკან ვაბრუნებთ. ვთქვათ, ასეთი წესით მივიღეთ 1000 შერჩევა რომელთაგან თითოეულში შერჩევის მოცულობა 30-ის ტოლია. პირველი 4 შერჩევა წარმოდგენილია 4 ფოთლებიანი ღეროების მსგავსი დიაგრამით:
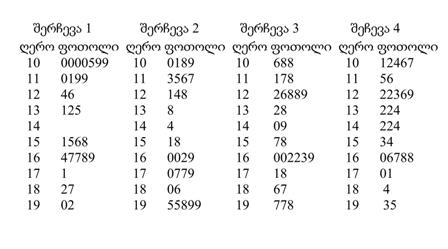
შერჩევებში 30 შემთხვევით ამოღებული ბურთულების ნომრებია 100-დან 199-მდე.
პირველი შერჩევის 30 მონაცემის საშუალოა -
მეორე შერჩევის საშუალოა -
მესამე შერჩევის საშუალოა -
მეოთხე შერჩევის საშუალოა -
ყველა მიღებული საშუალო ბევრად არ განსხვავდება პოპულაციის საშუალოსგან, რომელიც (100+101+102+ ...+198+199 )/100 = 149.5-ის ტოლია. 1000 შერჩევის საშუალოებით აგებული პოლიგონი ძალიან ახლოს იქნება ნორმალური განაწილების მრუდთან საშუალოთი. ცზთ-ის თანახმად, უნდა ყოფილიყო ზუსტად ასეთი სურათი.
პოპულაცია არ იყო ნორმალური, მაგრამ საშუალოების განაწილება დაემსგავსა ნორმალურს. ბუნებრივია ისმის კითხვა, რამდენად დიდი უნდა იყოს შერჩევის მოცულობა n, რომ სრულდებოდეს ცზთ? ეს დამოკიდებულია შემთხვევითი სიდიდეების განაწილების ფორმაზე. თუ განაწილება სიმეტრიულია, საჭიროა ნაკლები n. მრავალი განაწილების ტიპისათვის საკმარისია n = 30 იმისათვის, რომ დამოუკიდებელი, ერთნაირად განაწილებული შემთხვევითი სიდიდეები ჯამის განაწილება ახლოს იყოს ნორმალურ განაწილებასთან.
***
გამოყენებული ლიტერატურა:
Field, A. (2013). Discovering Statistics Using IBM SPSS Statistics. SAGE Publications Ltd.
კისი, ჰ. (2008). სტატისტიკა სოციალურ მეცნიერებებში. სოციალურ მეცნიერებათა ცენტრი. თბილისის უნივერსიტეტის გამომცემლობა
