მოსახერხებელია გაფანტულობის ოდნავ მოდიფიცირებული საზომის განხილვა, რომელსაც შესწორებულ შერჩევით დისპერსიას უწოდებენ$S_n^2=\frac{n}{b-1}{S}_n^2=\frac{1}{n-1}\underset{i=1}{\overset{n}{\sum (x_i-\overline{x}{)}^2=\frac{1}{n-1}\left[\sum _{i=1}^n{x}_i^2-n(\overline{x}{)}^2\right]}}$

შენიშვნა: აღსანიშნავია, რომ შერჩევითი საშუალოპოპულაციის საშუალოს საუკეთესო შეფასებაა, კერძოდ, იგი არის ე.წ. ჩაუნაცვლებელი შეფასება. ჩაუნაცვლებლობა გულისხმობს შემდეგს: მიუხედავად იმისა, რომ სხვადასხვა შერჩევის მიხედვით გამოთვლილი პარამეტრის შეფასება საზოგადოდ სხვადასხვა შედეგს იძლევა, ის საშუალოდ ემთხვევა პარამეტრის ჭეშმარიტ მნიშვნელობას. შერჩევითი დისპერსია არ არის პოპულაციის დისპერსიის საუკეთესო შეფასება, რადგან ის არ არის ჩაუნაცვლებელი. იმისათვის, რომ მიიღონ ჩაუნაცვლებელი შეფასება 1/n -ს ცვლიან 1/(n-1) -ით.

მოვიყვანოთ საილუსტრაციო მაგალითი იმისა, რომ შერჩევითი საშუალო ჩაუნაცვლებელი შეფასებაა, ხოლო შერჩევითი დისპერსია კი არ არის ჩაუნაცვლებელი. დავუშვათ, რომ პოპულაცია 3 მონაცემს შეიცავს {0, 2, 4} და მისგან ვაკეთებთ 2 მონაცემიან (n=2 მოცულობის) შერჩევებს. ცხადია, რომ პოპულაციის საშუალო იქნება $\mu =\frac{0+2+4}{3}=2$ ხოლო დისპერსია კი ${\sigma }^2=\frac{1}{3}\left[(x_1-\mu {)}^2+(x_2-\mu {)}^2+(x_3-\mu {)}^2\right]=\frac{1}{3}\left[(0-2{)}^2+(2-2{)}^2+(4-2{)}^2\right]=\frac{8}{3}$ ყველა შესაძლო ორმოცულობიანი შერჩევების რაოდენობა იქნება (შერჩევის როგორც პირველი, ისე მეორე ელემენტის შესაძლო მნიშვნელობათა რაოდენობა 3-ის ტოლოა). ამოვწეროთ ეს შერჩევები და გამოვთვალოთ მათი საშუალოები და დისპერსიები. ვისარგებლოთ ქვემოთმოყვანილი ცხრილით. 

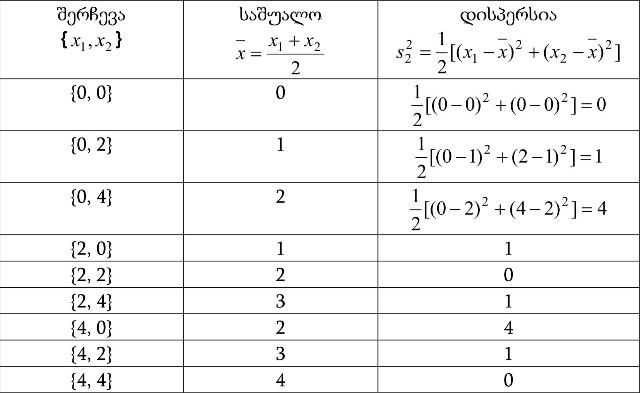
აქედან გამომდინარე, შერჩევითი საშუალოების საშუალო $\frac{0+1+2+1+2+3+2+3+4}{9}=2$ იქნება, ხოლო დისპერსიების საშუალო კი $\frac{0+1+4+1+0+1+4+1+0}{9}=\frac{4}{3}$ როგორც ვხედავთ, შერჩევითი საშუალო პოპულაციის საშუალოს ჩაუნაცვლებელი შეფასებაა, შეჩევითი დისპერსია კი პოპულაციის დისპერსიის არა. სინამდვილეში  $\frac{4}{3}=\frac{2-1}{2}·\frac{8}{3}=\frac{n-1}{n}·\frac{8}{3}$ და შესწორება ხდება სწორედ $\frac{n-1}{n}$-ის შებრუნებული სიდიდით $\frac{n}{n-1}$ რათა მივიღოთ ჩაუნაცვლებელი შეფასება $\frac{8}{3}=\frac{n}{n-1}\frac{4}{3}$ შევნიშნოთ, რომ თუ პოპულაციის საშუალო $\mu$ ცნობილია, მაშინ შერჩევითი დისპერსია განისაზღვრება ფორმულით $S_n^2=\frac{1}{n}\sum _{i=1}^n(x_i-\mu {)}^2$. უცნობი საშუალოს შემთხვევაში კი ვსარგებლობთ შერჩევითი საშუალოთი. მაგრამ როგორც ცნობილია (საშუალოს თვისება) $\sum _{i=1}^n(x_i-\overline{x}{)}^2\le \sum _{i=1}^n(x_i-\mu {)}^2$ ანუ $x_i$-ები უფრო ახლოსაა $\overline{x}$-თან, ვიდრე $\mu$-სთან. ამის საკომპენსაციოდ  $S_n^2$-ის ფორმულაში n-ის ნაცვლად გამოიყენება  n-1.

მოვიყვანოთ შერჩევითი დისპერსიის თვისებები:

1. თუ არსებული $x_1,x_2...x_n$  მონაცემებიდან შევქმნით ახალ მონაცემებს  $y_i=a{x}_i+b,i=1,2...,n$მაშინ $S_{\gamma }^2={\alpha }^2{S}_x^2$ და${S^2}_y=a^2{S^2}_x$

2. თუ  $x_1, x_2, ...x_n$ და $y_1,y_2,...y_m$ ორი შერჩევაა. მაშინ გაერთიანებული შერჩევისათვის $x_1,x_2,...x_n, y_1, y_2, ....y_m$  შერჩევითი დისპერსია და შესწორებული დისპერსია გადაითვლება შემდეგნაირად:  $S_{n,m}^2=\frac{n}{n+m}{S}_x^2+\frac{m}{m+n}{S}_y^2+\frac{mn}{(m+n{)}^2}(\overline{x}-\overline{y}{)}^2$  და $S_{n,m}^2=\frac{n-1}{n+m}{S}_x^2+\frac{m-1}{m+n}{S}_y^2+\frac{mn}{(m+n-1)(m+n)}(\overline{x}-\overline{y}{)}^2$

იმ კერძო შემთხვევაში, როცა n=m და $\overline{x}=\overline{y}$ გაერთანებული შერჩევის შერჩევითი დისპერსია იქნება $S^2=(S_x^2+S_{\gamma }^2)/2$.

***

გამოყენებული ლიტერატურა:

Field, A. (2013). Discovering Statistics Using IBM SPSS Statistics. SAGE Publications Ltd.

კისი, ჰ. (2008). სტატისტიკა სოციალურ მეცნიერებებში. სოციალურ მეცნიერებათა ცენტრი.  თბილისის უნივერსიტეტის გამომცემლობა